

The Prosa framework is built on top of the Coq proof assistant and the ssreflect extension from the Mathematical Components library.
Coq is a proof assistant based on a higher-order logic with support for computation. That is, apart from writing specifications and proving theorems, in Coq it is also possible to write programs (as recursive functions) and prove claims about them.
Prosa uses the computational capabilities of Coq to implement schedulability analyses, and then states and proves schedulability claims about the implemented analyses (e.g., of the form “if this algorithm returns ‘no deadline missed’, then there does not exist a schedule matching the stated assumptions in which a deadline is missed”).
Ssreflect, in turn, is an extension for Coq that originated in the development of the formal proof of the Four Color Theorem. Apart from several improvements in the proof tactics, ssreflect includes many libraries for mathematical reasoning. One of these libraries, bigop, is used pervasively throughout Prosa to declare LaTeX-like operators such as \sum.
To install Coq and ssreflect on your computer, please follow the setup instructions.
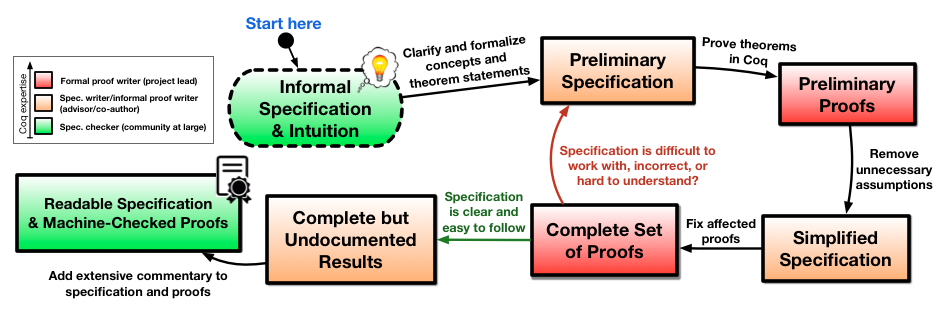
There are three basic ways of working with Prosa, each of which requires different levels of expertise in Coq.
Specification Reader (one-day crash course in Coq): By reading the specification, one can check whether Prosa’s formalization of real-time scheduling concepts matches the view informally agreed upon by the real-time community or the specific assumptions in a particular paper. This is a crucial role — the trust in the formal proofs derives from the fact that the specification is read, and deemed to be reasonable, by as many experts as possible. Prosa’s goals and principles are intended to make this task as easy as possible.
Anyone with a background in real-time scheduling and informal logic should be able to quickly pick up the essential syntax needed to read the specification in a matter of a few hours. To get started, read the essential syntax primer below.
Specification Writer (basic experience with Coq): The specification writer is responsible for writing and critiquing definitions, theorem statements, and commentary, all of which compose the “external view” of Prosa that is intended to be read and checked by specification readers. Another important task that specification writers help with is to organize and subdivide the overall proof outline into (many) simple, intermediate lemmas (i.e., to help break the proof into small steps), to clearly expose the high-level strategy and the underlying intuition of the proof to readers.
Someone who is already comfortable with functional programming and precise mathematical specifications can acquire the minimal Coq background needed to get started as a specification writer in a few days. Obviously more time is required for someone coming from a more distant background.
Proof Writer (extensive experience with Coq): The proof writer is responsible for proving the theorems and lemmas, and for guiding the specification writers. Since misconceptions about the model (e.g., insufficient or mismatching assumptions) tend to become apparent only when writing proof scripts, there must be a constant feedback cycle and collaboration between proof writers and specification writers.
Writing proof scripts is not trivial and requires some familiarity with Coq and ssreflect, which realistically takes a couple of months to become fluent (see proof prerequisites).
Based on our experience with Prosa, this division naturally maps to a workflow in which co-authors of various levels of Coq expertise collaborate to develop formal proofs, as illustrated in the figure below.
In the following, we provide a short guide for reading specifications in Prosa.
Note: this primer is still a work in progress; feedback, improvements, and corrections are very welcome.
Assumptions in Coq can be stated with the keyword Hypothesis. For example, this is how we assume that tasks have constrained deadlines.
Prosa makes extensive use of Coq’s Hypothesis feature to make all assumptions explicit.
In Coq, a Definition creates an alias to an expression. For example, the following statement defines a pending job as a job that has arrived but has not yet completed.
Here, the name pending is bound to a function with a parameter t of type time.
Prosa uses definitions extensively to define simple predicates, which usually are defined in terms of simpler predicates. For example, pending is defined in terms of the more basic notions of has_arrived j t (the job #j# is released on or prior to time #t#) and ¬ completed t (the job #j# is not yet complete at time #t#).
In Coq, lemmas, theorems, corollaries, remarks, and facts are all the same thing: aliases to proof terms. A Lemma, for example, can be declared as follows. (For simplicity, some variables from the context are omitted.)
Note that Coq only allows a lemma to be declared if a correct proof is provided.
In Coq, a Section creates a scope wherein variables can be instantiated and/or constrained.
The variables introduced in a section are defined only within the scope of the section. By default, variables are entirely unrestricted: every variable is universally quantified, i.e., there is an implied “for all possible values”.
Generality can be restricted within a section by explicitly stating assumptions. For example, in the shown segment, the claim is restricted to apply only to schedules (any sched) in which jobs cease to execute after having received an amount of processor service equal to their execution cost (as determined by job_cost).
Any definition or lemma stated within the section can be accessed from outside, under two conditions:
when reusing definitions and lemmas, any variable declared in the section must be passed explicitly, and
when reusing lemmas only, any stated hypothesis must be supplied (i.e., proven to hold in the external context).
In the example above, this means that we can only use the proven lemma outside this section if we supply both a proof of the hypothesis that “completed jobs do not execute” and some job #j# to be considered.
Finally, note that Coq keeps track of the dependencies across definitions and lemmas. Therefore, there is no need to supply hypotheses that are not used by the lemmas we want to access, even if such hypotheses are redundantly assumed in the corresponding section.
The library bigops from ssreflect allows defining arbitrary functions based on summation (#\sum#), product (#\prod#), and any other customized operator. This provides a natural and clear notation for definitions that might otherwise require ad hoc recursion.
One example of the use of bigop is our definition of instantaneous service of a job, which just counts the number of processors where a job is scheduled.
The rest of this guide is concerned with developing new proofs.
To develop proofs in Prosa, there are two prerequisites. First, one must know how to prove theorems in Coq (i.e., apply lemmas, perform case analysis, use induction, etc.). After that, one should learn the basics of ssreflect (tactics, boolean reflection and the libraries used by Prosa). To help with this process, we recommend some study material for learning Coq and ssreflect.
For a gentle Coq tutorial, we recommend the first couple of chapters of the Software Foundations book by Pierce et al., available for free on their webpage. The final chapters of the book (starting from Imp: Simple Imperative Programs) cover programming languages semantics and can be safely ignored (in the context of Prosa).
Alternatively, one can also read the Mathematical Components book, which introduces Coq in the context of the Mathematical Components library, thus with the same syntax used by Prosa.
Other sources for documentation and guides are listed on the Coq webpage.
Ssreflect can be learned in two steps: (1) getting used to the new tactics and notation, and (2) learning the new mathematical theories (definitions and lemmas).
For an introduction to the new tactics, please refer to the Mathematical Components book and the Ssreflect manual. Moreover, some examples are also given in the tutorial that was held at the Advanced Coq Winter School.
To learn the new theories, note that the core of Prosa uses only six of the basic ssreflect libraries:
ssrbool: a theory of boolean predicates, boolean reflection and relations.
ssrnat: a theory of natural numbers.
div: a theory of natural division and divisibility.
fintype: a theory of finite types, e.g., ordinals (bounded natural numbers).
seq: a theory of finite sequences (lists).
bigop: a theory for LaTeX-like operators (\sum, \max, etc.)
This limited scope makes it possible to learn Prosa by studying and emulating the existing proofs while ignoring the more complex parts of Mathematical Components; to this end, reading the coqdoc documentation of the existing Prosa proofs is helpful. For additional material, please check the Mathematical Components book and the tutorials from ITP13 (see also the video) and the Advanced Coq Winter School.
Even after learning how to use the libraries, carrying out mechanized proofs requires some practice, so please feel free to send questions to our mailing list in case of problems.